Constructive Solid Geometry#
Constructive solid geometry (CSG) is the process of combining a set of initial, often simple geometries into more complex shapes through the use of boolean operations such as unions, intersections, and differences [LTH86]. In computer graphics applications, this may involve ray tracing or other approaches for efficient visualization, but MyMesh is primarily concerned with generating and/or modifying meshes. MyMesh offers two approaches to CSG: implicit and explicit.


Implicit CSG#
For implicit CSG, boolean operations are performed on implicit functions or a
set of values evaluated at points in a grid or mesh (e.g. image data). Performing
boolean operations in this way is quite efficient, but a contouring step is
required to generate a mesh, which may result in a loss of detail at sharp
features or interfaces. In MyMesh, implicit CSG operations rely on
mymesh.implicit and mymesh.contour.
Boolean operations can be performed directly on the functions to obtain a new
implicit function. implicit offers several sets of boolean
operator functions depending on what type of data is being operated on: arrays
of values (union(), intersection(),
diff()), functions (unionf(),
intersectionf(), difff()), or
sympy-based functions (unions(),
intersections(), diffs()). This
new function can then be meshed as any other implicit function.
func1 = implicit.box(-.9,.9,-.9,.9,-.9,.9)
func2 = implicit.sphere([0,0,0],1)
func = implicit.difff(func1, func2)
diff = implicit.SurfaceMesh(func, [-1,1,-1,1,-1,1], .05)
diff.plot(bgcolor='w',view='trimetric')

While this approach is straight forward and efficient, it suffers from some of the classic limitations of implicit meshing, particularly, poor resolution along the sharp edges introduced by the intersection of the two objects (though more advanced contouring methods can alleviate these).
Another approach is to generate a tetrahedral mesh of the first object and then contour the second function using the first mesh as a background mesh. Here, the threshold direction needs to be chosen appropriately to achieve the intended operation (and a union operations are more difficult to achieve).
func1 = implicit.box(-.9,.9,-.9,.9,-.9,.9)
func2 = implicit.sphere([0,0,0],1)
cube = implicit.TetMesh(func1, [-1,1,-1,1,-1,1], .05)
diff = implicit.TetMesh(func2, [-1,1,-1,1,-1,1], .05, background=cube, threshold_direction=1)
diff.plot(bgcolor='w',view='trimetric')

This operation can equivalently be performed using the
Contour() method.
m1.NodeData['func2'] = func2(m1.NodeCoords[:,0], m1.NodeCoords[:,1], m1.NodeCoords[:,2])
m2 = m1.Contour('func2', 0, threshold_direction=1, Type='vol')
This leads to much cleaner intersection edges between the two objects, however repeated contouring of a tetrahedral mesh can lead to low quality tetrahedra that may require improvement if being used for finite element applications.
Explicit CSG#
Explicit CSG operates directly on existing meshes, rather than functions or
values. This involves calculating intersections between meshes (utilizing
mymesh.rays and mymesh.tree) and then splitting and joining
elements to create the new mesh. These operations are more computationally
demanding and generally slower than implicit CSG, especially for large meshes,
but and can be used when no functional representation of a mesh exists.
Floating point errors in the identification of intersections and
splitting of elements can result in mesh defects and unclosed surfaces, which
may be problematic for some applications. If performing explicit CSG on surface
meshes with the aim of producing models that require volumetric meshes,
fTetWild may be useful for
generating high quality tetrahedral meshes from imperfect surfaces
[HSW+20]. Explicit CSG mesh boolean functions can be found in
mymesh.booleans.
Since the vast majority of the computational effort is spent splitting and
labeling elements, which is done identically regardless of which operation is
being performed, MeshBooleans() returns the union,
intersection, and difference meshes together (note that the difference is not
symmetric, i.e. A-B ≠ B-A).
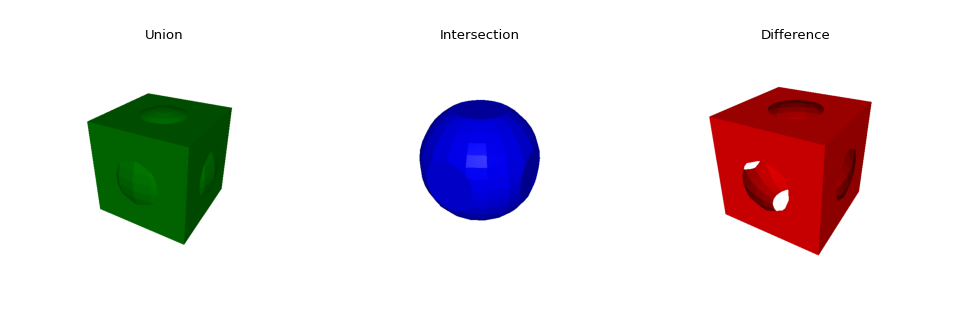
cube = primitives.Grid([-.9,.9,-.9,.9,-.9,.9], .25, Type='surf', ElemType='tri')
sphere = primitives.Sphere([0,0,0], 1, ElemType='tri')
U,I,D = booleans.MeshBooleans(cube,sphere)
# Plotting:
fig1, ax1 = U.plot(show=False,return_fig=True,color='g',bgcolor='w',view='trimetric')
fig2, ax2 = I.plot(show=False,return_fig=True,color='b',bgcolor='w',view='trimetric')
fig3, ax3 = D.plot(show=False,return_fig=True,color='r',bgcolor='w',view='trimetric')
plt.close(fig1); plt.close(fig2); plt.close(fig3);
fig, (a1, a2, a3) = plt.subplots(1, 3, figsize=(12,4))
a1.imshow(ax1.get_images()[0].get_array())
a2.imshow(ax2.get_images()[0].get_array())
a3.imshow(ax3.get_images()[0].get_array())
a1.set_title('Union')
a1.set_axis_off()
a2.set_title('Intersection')
a2.set_axis_off()
a3.set_title('Difference')
a3.set_axis_off()
plt.tight_layout()
plt.show()